Por PGAPereira. A maioria
das formas de contar e medir as coisas funciona de maneira lógica. Mas as
coisas não são tão sensíveis em astronomia - pelo menos não quando se trata do brilho das estrelas.
A história começa por volta de 129 aC, quando o astrônomo grego Hiparco
produziu o primeiro catálogo de estrelas conhecido. Hiparco classificou suas
estrelas de uma forma simples. Ele chamou as mais brilhantes "de primeira
grandeza", significando apenas "a maior". As estrelas não tão
brilhantes ele as chamou "de segunda grandeza", ou a segunda maior.
As estrelas mais fracas que ele podia ver ele chamou "de sexta
magnitude." Por volta de 140 dC, Cláudio Ptolomeu copiou este sistema em
sua própria lista de estrelas. Às vezes, Ptolomeu acrescentou a palavra “maior”
ou “menor” para distinguir entre as estrelas dentro de uma classe de magnitude.
As obras de Ptolomeu mantiveram os textos básicos de astronomia pelos 1.400
anos seguintes, para que todos usassem o sistema de primeira a sexta
magnitudes. Funcionou muito bem. Galileu forçou a primeira mudança. Ao soerguer
seus telescópios recém-feitos para o céu, Galileu descobriu que as estrelas que
existiam eram mais fracas que a sexta magnitude de Ptolomeu. "De fato, com
a objetiva que você irá detectar as estrelas abaixo da sexta magnitude como uma
multidão de outras que escapam à vista natural que é pouco crível", ele
exultou em seu trato 1610 Sidereus Nuncius ". A maior delas ... nós
podemos designar como de sétima magnitude. " Assim, um novo termo surgia na linguagem astronômica, e tornou-se a escala
de magnitude em aberto. Não poderia haver volta.
Quando os telescópios
ficaram maiores e mais precisos, os astrônomos continuaram adicionando mais
magnitudes ao fundo da escala. Hoje, um par de binóculos de 50 milímetros
permite ver estrelas de cerca de magnitude 9, um telescópio amador de 6
polegadas vai atingir magnitude 13, e o Telescópio Espacial Hubble já viu
objetos tão tênue quanto de magnitude 31. Em meados do século XIX, os
astrônomos perceberam que havia uma necessidade premente de definir toda a
escala de magnitude, mais precisamente do que, por decisão do globo ocular.
Eles já tinham determinado que uma estrela de primeira magnitude brilhasse com
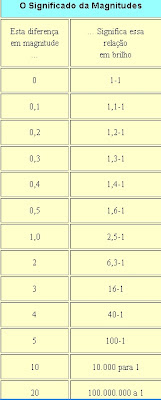
cerca de 100 vezes a luz de uma estrela de magnitude 6. Assim, em 1856 o astrônomo
de Oxford, Norman R. Pogson propôs que uma diferença de cinco magnitudes ser exatamente
definida como um razão de brilho de 100 para 1. Esta regra conveniente foi
rapidamente adotada. Uma magnitude corresponde assim a uma diferença de brilho exatamente
da raiz quinta de 100, ou muito perto de 2,512 - um valor conhecido como a
razão de Pogson. A escala de magnitude resultante é logarítmica, de
acordo com a crença pura de 1850, que todos os sentidos humanos são
logarítmicos na sua resposta a estímulos. A escala de decibéis para a avaliação
de loudness foi feita da mesma forma logarítmica.
Infelizmente, não é bem assim, nem
para o brilho, som ou qualquer outra coisa. Nossas percepções do mundo seguem
leis de potência curvas, não as logarítmicas. Assim, uma estrela de magnitude
3,0 de fato não está exatamente a meio caminho de brilho entre 2,0 e 4,0.
Parece um pouco mais fraca do que isso. A estrela que parece está a meio
caminho entre 2,0 e 4,0 será de cerca de magnitude 2,8. Quanto maior o hiato da
magnitude, maior é a discrepância. Assim os mapas do céu desenhados por
computador da Sky & Telescope usa pontos como estrelas que são
dimensionados de acordo com uma relação de lei da potência.Mas o mundo
científico em 1850 era dominado por logaritmos, então agora eles estão presos
no sistema de magnitude tão firmemente quanto a numeração de Hiparco na
antiguidade. Agora que magnitudes estelares foram classificadas em uma escala
matemática precisa, no entanto mal ajustadas, outro problema tornou-se
inevitável. Algumas estrelas de "primeira magnitude" eram muito mais
brilhante que todas as outras. Os astrônomos não tinham escolha a não ser
estender a escala para valores mais brilhantes, bem como as fracas. Assim
Rigel, Capella, Arcturus, Vega são de magnitude 0, uma declaração que soa
estranha como se elas não tivessem brilho algum! Mas era tarde demais para
começar de novo. A escala de magnitude se estende mais para números negativos:
Sirius brilha com magnitude -1,5, -4,4 chega Venus, a Lua cheia é de cerca de
-12,5, e as chamas do Sol em magnitude -26,7.
No final do século 19 os
astrônomos estavam usando a fotografia para registrar o céu e medir o brilho das
estrelas, e um novo problema surgiu. Algumas estrelas que mostravam o mesmo
brilho para o olho mostrou brilhos diferentes em filmes, e vice-versa. Em
comparação com o olho, as emulsões fotográficas eram mais sensíveis à luz azul
e menos a luz vermelha. Assim, duas escalas separadas foram criadas. Magnitude
Visual, ou m vis, descrita como uma estrela vista pelos
olhos. Magnitude fotográfica, ou m pg, referindo-se a imagens de estrelas em azul-sensível a filme
preto-e-branco. Estes são agora abreviados m V e M p,
respectivamente.
Esta complicação acabou por ser uma
bênção disfarçada. A diferença entre a magnitude fotográfica e visual de uma
estrela era uma medida conveniente da cor da estrela. A diferença entre os dois
tipos de magnitude foi nomeada "índice de cor." Seu valor é cada vez
mais positivo para estrelas amarelas, laranjas e vermelhas, e negativo para as
azuis. Mas diferentes emulsões fotográficas têm diferentes respostas
espectrais! E os olhos das pessoas diferem muito. Por um lado, as lentes de seus
olhos ficam amarelas com a idade, as pessoas velhas vêem o mundo através de
filtros amarelos. Sistemas de magnitude concebidos para gamas de comprimento de
onda diferentes tiveram de ser mais claramente definida do que este. Hoje,
magnitudes precisas são especificadas por um fotômetro fotoelétrico padrão que
vê através de filtros de cores padrão. Vários sistemas fotométricos foram concebidos;
o mais familiar é chamado UBV após os três filtros mais comumente utilizados. U
abrange a quase ultravioleta, B é azul, e V corresponde bem de perto à antiga magnitude
visual; seu pico está na faixa verde-amarela, onde o olho é mais sensível. Índice de cor é agora definido como a magnitude B menos a magnitude V. A estrela branca pura tem um BV de cerca de 0,2, o nosso Sol amarelo é de 0,63, a laranja-vermelho Betelgeuse é de 1,85, e as estrelas mais azuis acreditava-se possível ser -0,4, azul-branco pálido. Tão bem sucedido foi o sistema UBV que foi prorrogado para o vermelho,redward com R e filtros para definir padrão de magnitudes no vermelho e infravermelho próximo. Por isso, é algumas vezes chamado UBVRI. Os astrônomos infravermelhos efetuaram comprimentos de onda ainda mais longos, acrescentando ordem alfabética após a letra I para definir as bandas J, K, L, M, N e Q. Estas foram escolhidas para combinar com as “janelas” dos comprimentos de onda do infravermelho na atmosfera da Terra - comprimentos de onda em que o vapor de água absorve não inteiramente a luz das estrelas. Brilhando em todas as faixas de freqüências, a estrela Vega foi escolhida (arbitrariamente) para definir a magnitude 0,0. Visto que Vega é mais opaca no infravermelho do que na luz visível, as magnitudes infravermelhas são, por definição e bastante artificialmente, "brilhantes" do que suas contrapartes visuais.
Foto-5-D. No Mapa da esquerda de Canis
Major os diâmetros das esferas indicam as Magnitudes Aparentes das estrelas,
os pontos correspondem aos brilhos das estrelas que vemos. A versão da direita
indicam as Magnitudes Absolutas das mesmas estrelas quanto brilhante apareceriam se todas elas
fossem colocadas à mesma distância da Terra (32,6 anos-luz). Magnitude absoluta
é uma medida da luminosidade verdadeira da estrela.
O que é então o brilho verdadeiro de um objeto? Quanta energia
total é enviada para nós em todos os comprimentos de onda combinados, visível e
invisível? A resposta é chamada de magnitude bolométrica, m bol,
isto porque antigamente a radiação total era medida com um dispositivo chamado
bolómetro. A magnitude bolométrica dá o brilho verdadeiro de um objeto. O
astrofísico considera como a verdadeira medida da emissão total de energia de
um objeto, visto da Terra. A correção bolométrica diz quanto maior o
brilho na magnitude bolométrica, maior é que a magnitude V. Seu valor é sempre negativo,
porque qualquer estrela ou objeto que emite radiação, pelo menos, alguns fora
da parte visual do espectro eletromagnético. Até agora temos vindo a lidar
apenas com magnitude aparente - como as coisas brilhantes são vistas a
partir da Terra. Nós não sabemos como intrinsecamente brilhante um objeto é até
nós também levarmos em conta a sua distância. Assim, os astrônomos criaram a
escala de magnitude absoluta. A magnitude absoluta de um objeto é
simplesmente o brilho que ele teria se colocado a uma distância padrão de 10
parsecs (32,6 anos-luz).
Visto desta distância, o Sol irá
brilhar em uma inexpressiva magnitude visual 4,85. Rigel iria brilhar em uma
deslumbrante -8, quase tão brilhantes como a Lua. A anã vermelha Proxima
Centauri, a estrela mais próxima do sistema solar, parece ter magnitude 15,6, o menor vislumbre pouco
visível em um telescópio de 16 polegadas! Saber as magnitudes absolutas deixa
claro como extremamente diversificada são os objetos que casualmente fixam-se
juntos sob a única palavra "estrela". Magnitudes absolutas são sempre
escritas com M maiúsculo e uma magnitude aparente com m
minúsculo. Qualquer tipo de magnitudes aparente, fotográfica, bolométrica, ou o
quer que seja - pode ser convertida em magnitude absoluta. (Para cometas e
asteróides, "magnitudes absolutas" muito diferentes são usadas. O
padrão aqui é quão brilhante o objeto pareceria para um observador em pé, se o
objeto estivesse colocado a uma unidade astronômica de distância do Sol.) Então,
o sistema de magnitude é muito
complicado? Nem um pouco. Ele cresceu e evoluiu para preencher todas as
necessidades de medição de brilho, exatamente conforme necessário. Hipparcus
ficaria encantado.
Nenhum comentário:
Postar um comentário